The adaptive filter is a digital filter that can automatically adjust the performance according to the input signal for digital signal processing. In contrast, non-adaptive filters have static filter coefficients that together make up the transfer function.
For some applications, adaptive parameters are required for processing because they do not know in advance the parameters that need to be manipulated, such as the characteristics of some noise signals. In this case, an adaptive filter is typically used, which uses feedback to adjust the filter coefficients as well as the frequency response.
In general, the adaptive process involves using a cost function to determine how to change the filter coefficients to reduce the cost of the next iteration process. The value function is a criterion for determining the optimal performance of the filter, such as the ability to reduce the noise component of the input signal.
As the performance of digital signal processors has increased, the use of adaptive filters has become more common, and today they are widely used in mobile phones and other communication devices, digital video recorders and digital cameras, and medical monitoring devices.
The block diagram shown below is the basis for the implementation of special adaptive filters such as Least Mean Square Filter (LMS) and Re: Recursive least squares filter (RLS, which we usually call the least squares method). The theoretical basis of the block diagram is that the variable filter can obtain an estimate of the desired signal.
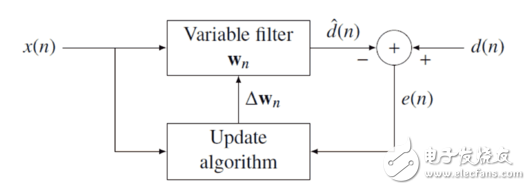
1) System identification: At this time, the reference signal is the output of the unknown system. When the error is minimum, the adaptive filter has similar characteristics to the unknown system. The adaptive filter is used to provide a best in a sense. Fitting a linear model of an unknown device
2) Inverse model: In this type of application, the role of the adaptive filter is to provide an inverse model that best fits the unknown noise device in a sense. Ideally, in the case of a linear system, the inverse model has a transfer function equal to the inverse of the transfer function of the unknown device, such that the combination of the two constitutes an ideal transmission medium. The delay entered by the system constitutes the desired response of the adaptive filter. In some applications, the system input is used as the desired response without delay.
3) Prediction: In such applications, the role of the adaptive filter is to provide a best prediction of the current value of the random signal. Thus, the current value of the signal is used as the desired response of the adaptive filter. The past value of the signal is applied to the input of the filter. Depending on the application of interest, the output or estimation error of the adaptive filter can be used as the output of the system. In the first case, the system acts as a predictor; in the latter case, the system acts as a predictive error filter.
4) Interference cancellation: In a class of applications, the adaptive filter eliminates unknown interference contained in the fundamental signal in a manner that is optimized. The base signal is used as the desired response of the adaptive filter and the reference signal is used as the input to the filter. The reference signal comes from a certain sensor or group of sensors that are located and is supplied to the basic signal in such a way that the signal carrying the innovation is weak or substantially unpredictable.
That is to say, the desired output is often not the purpose of introducing an adaptive filter. The purpose of introducing it is to obtain the unknown system model, obtain the reciprocal of the transfer function of the unknown channel, obtain the future signal or error, and get the original signal to eliminate the interference.
Adaptive filtering is the approximation of a mixed signal to a desired signal. In the process of approximation, according to the uniformity error (MSE) of the observed signal and the real (expected) signal as the quantitative index, iterative according to certain rules (the iterative rule itself can be set) until the algorithm converges (the convergence conditions are many, such as Achieve a preset number of iterations, or reach an allowable error, etc.). The existing common adaptive algorithms are RLS, LMS, and NLMS, which are often iterated according to the gradient descent method or Newton method.
Algorithm backgroundClassical filtering algorithms include Wiener filtering and Kalman filtering. These filtering algorithms need to estimate the correlation coefficient, noise power and other parameters of the input signal. In practice, it is difficult to accurately estimate these parameters, and accurate estimation of these parameters. Directly affects the filtering effect of the filter. On the other hand, the two types of filters are generally designed and the parameters cannot be changed. In practical applications, it is desirable that the parameters of the filter can be changed as the input signal changes to achieve better real-time processing results. In order to make up for the shortcomings of the traditional filtering algorithm and meet the requirements of signal processing, adaptive filtering has been developed.
Basic principle of algorithmThe biggest difference between adaptive filtering and Wiener filtering, Kalman filtering is that there is a feedback channel between the output and the filtering system. The coefficient of the filter is adjusted according to the error of the output of the filter and the expected signal at a certain time. Thereby, the dynamic adjustment of the filter coefficients is realized, and optimal filtering is realized.
(1) Signal model
The purpose of adaptive filtering is still to extract the true and accurate expected signal from the observed signal, so the signals involved are:
Expected signal d(n)
Input signal x(n)=d(n)+v(n)
Output signal y(n)
(2) Algorithm principle
An M-order filter with a coefficient of w(m), the output is:
y(n)=Σw(m)x(nm) m=0...M
Write in matrix form: y(j)=WT(j)*X(j)
The output error at time n is: e(j)=d(j)-y(j)= d(j)- WT(j)*X(j)
To define the objective function as E[e(j)^2], then:
J(j)=E[e(j)^2]= E[(d(j)- WT(j)*X(j))^2]
When the above error reaches a minimum, optimal filtering is achieved, and the objective function determines the minimum variance adaptive filtering.
For the objective function J(j), it is required to take the W corresponding to the minimum value, where the gradient descent method is used for optimization:
W(j+1)=W(j)+1/2*μ(-▽J(j))
â–½J(j)=-2E[X(j)*( d(j)- WT(j)*X(j))]= -2E[X(j)e(j)]
W(j+1)=W(j)+μE[X(j)e(j)]
Where -2X(j)e(j) is called the instantaneous gradient, because the instantaneous gradient is an unbiased estimate of the true gradient, where the instantaneous gradient can be used instead of the true gradient.
W(j+1)=W(j)+μX(j)e(j)
Thus, an iterative formula for adaptively filtering the optimal coefficients can be obtained.
Shenzhen Sunbeam New Energy Co., Ltd , https://www.sunbeambattery.com